连续变量单点概率
在本课的下一部分,Sebastian Thrun 将向你介绍连续变量,连续概率分布及其背后的含义。
如之前所述,连续变量可以采用任何实数,例如整数或小数。 即使是像圆周角度这样的变量也是连续的。

绕着轮盘旋转的箭头
该角度可以取任何十进制值,如 60.7423 度。 即使合理值的范围可能被限制在 0 到 360 度之间,角度也可以在该范围之间取任意小数。 你可以查看本课的下一部分,以了解更多详情。
下图显示的是子弹从抢射出后落在x的概率?
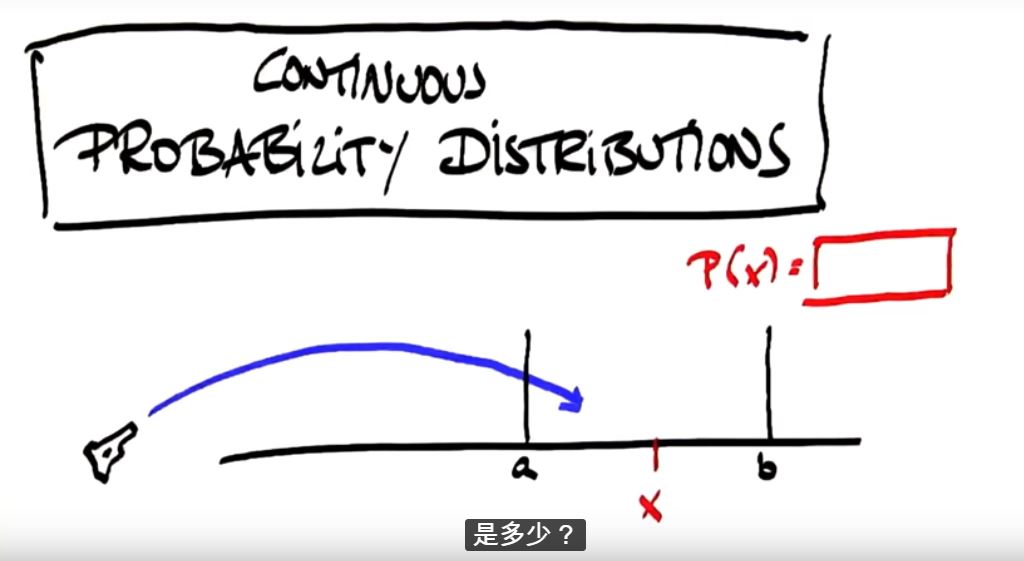
答案为0

可知连续事件的值在单点处的概率为0
连续变量区间概率

旋转酒瓶,瓶嘴在0到180度区间的概率为0.5.

连续概率分布
在本课的下一部分中,Sebastian 将介绍如何以连续的概率分布进行可视化和计算。 在你继续学习之前,让我们再次回顾并比较一下离散和连续分布。
在本课一开始,我们向你展示了一个连续概率分布旁边的离散概率分布。 如下图所示:

离散与连续概率分布
离散分布可以被分解成“片”。 每“片”代表一个结果,比如在硬币抛掷 3 次的例子中,有出现 0 次正面、 1 次正面、 2 次正面 和 3 次正面的不同情况 。
连续分布在整个 x 轴范围内都有一条连续不断的线。 比如,对于速度来说,你可以有 20 或 20.5 或 -10.451 的速度。
注意连续分布上的 y 轴标签:“概率密度函数”。 对于离散概率分布来说,y 轴表示事件发生的概率。 在连续情况下,概率密度函数并不直接表示概率; 相反,密度函数曲线下方的区域代表概率。
你将在本课的下一部分中了解更多信息。
不过,即使不知道“概率密度函数”意味着什么,你也可以从图表中了解到,速度大概在 20 左右,而速度大概在 0 或40 左右的可能性更小。
连续分布的特征
以下是连续分布和概率密度函数的一些特征。 在阅读本课的下一部分时,请牢记这些内容:
- y 值必须大于或等于 0。
- 发生于特定 x 值的概率可以等于 0。
- 两个 x 值之间发生事件的概率等于这两个 x 值之间的曲线下面积。
- 概率密度函数曲线下的总面积等于 1。
实际上,这些规则意味着速度等于 20 的概率为零。 对于连续分布,只能计算 19.99 和 20.01之间一系列值中的概率。
因为曲线下的总面积是 1,所以 “速度在负无穷和正无穷之间” 是有 100% 的可能性。